There are twelve (12) practice problems in this exercise about the area of the circle. You may use a calculator. Do not round intermediate calculations.
Round your final answer to two decimal places unless the exact answer is required.
For your convenience, I have included the different variations of formulas that you can use to find the area of a circle.
Problem 1: What is the area of a circle with radius [latex]8[/latex] meters? Leave your answer in terms of [latex]\large<\pi>[/latex].
This problem requires us to leave our answer in terms of [latex]\pi[/latex].
[latex]64\pi [/latex] square meters
Problem 2: The diameter of a circle is [latex]4.5[/latex] feet. Find its area. Use [latex]\pi = 3.1416[/latex].
[latex]15.90[/latex] square feet
Problem 3: Find the area of the circle below with a given radius. Use [latex]\pi = 3.14[/latex]
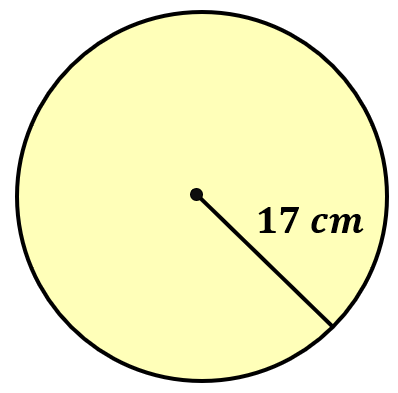
[latex]907.46[/latex] square centimeters
Problem 4: Find the area of the circle below with a given diameter. Use the value of [latex]\pi[/latex] on your calculator.
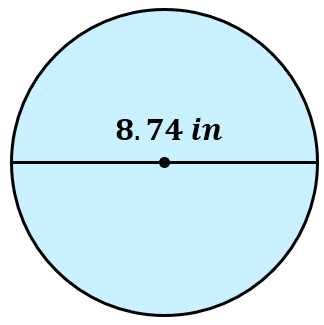
Make sure that you use the internal value of [latex]\pi[/latex] on your calculator.
[latex]60.00[/latex] square inches
Problem 5: The circumference of a circle is [latex]22.2[/latex] feet. What is its area? Use [latex]\pi = 3.14[/latex]
[latex]39.24[/latex] square feet
Problem 6: Determine the area of a dinner plate with a circumference of [latex]37.68[/latex] inches. Use [latex]\pi = 3.14[/latex].
[latex]113.04[/latex] square inches
Problem 7: The radius of a circle is [latex]5[/latex] inches. Find the area of the circle expressed in square centimeters [latex]c[/latex]. Use 1 in = 2.54 cm. Use [latex]\pi = 3.14[/latex].
Convert [latex]5[/latex] inches to centimeters.
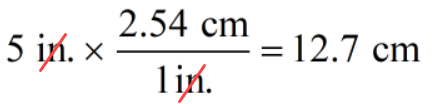
[latex]506.45[/latex] square centimeters
Problem 8: The diameter of a circle is [latex]12.4[/latex] miles. Calculate the area of the circle in terms of square kilometers [latex]k[/latex]. Use 1 mi = 1.609 km. Use [latex]\pi = 3.1416[/latex].
Convert [latex]12.4[/latex] miles to kilometers.
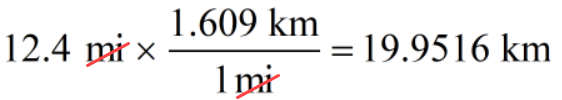
[latex]312.64[/latex] square kilometers
Problem 9: What is the radius of a circle with an area of [latex]73.12[/latex] square miles [latex]m[/latex]? Use [latex]\large <\pi = <<22>\over 7>>[/latex].
Problem 10: Determine the diameter of the circle having an area of [latex]100[/latex] square yards [latex]y[/latex]. Use [latex]\large <\pi = <<22>\over 7>>[/latex].
Problem 11: Find the area of the semicircle below with a diameter of [latex]8[/latex] centimeters. Use [latex]\pi = 3.1416[/latex].
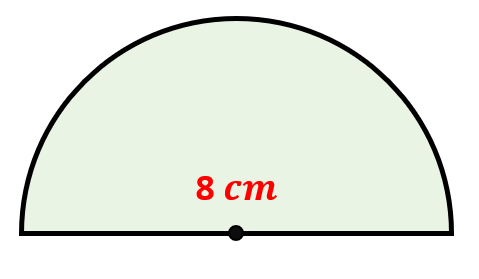
The area of a semicircle is half of the area of a circle.
[latex]27.33[/latex] square centimeters
Problem 12: Both circles share the same center. Find the exact area of the shaded region.
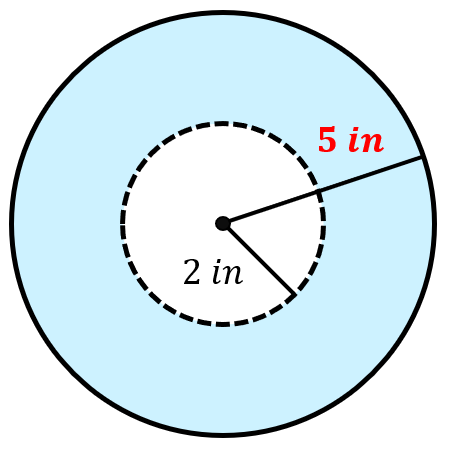the same center. the radius of the smaller circle is 2 inches while the larger circle is 5 inches." width="456" height="451" />
Area of the shaded region = area of the larger circle minus area of the smaller (inner) circle
[latex]21\pi [/latex] square inches
You might also like these tutorials:
Categories
